Pengertian
Matriks merupakan
Suatu alat atau sarana yang sangat ampuh untuk menyelesaikan model-model linier.
Definisi Matriks adalah
Susunan empat persegi panjang atau bujur sangkar dari bilangan-bilangan yang diatur dalam baris dan kolom ditulis diantara dua tanda kurung, yaitu ( ) atau [ ]
Elemen matriks : aij
Susunan bilangan atau nilai aij {bilangan real atau kompleks}
Ukuran matriks :
Jumlah baris : m
Jumlah kolom : n
Ordo atau ukuran matriks : m x n
Elemen-elemen diagonal : a11, a22,….,ann
Notasi matriks, menggunakan huruf besar (kapital)
Kesamaan matriks
Matriks A = (aij)
B = (bij)
contoh
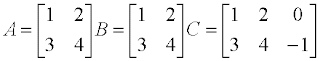
A = B jika aij = bij untuk semua
i = 1, 2 .. m dan j = 1, 2,...n
A = B
A C (ukurannya tidak sama)
Matriks A dan Matriks B disebut sama, bila
Ordo-ordonya sama
Elemen-elemen yang seletak sama
Bentuk Matriks Khusus
Matriks bujur sangkar
Suatu matriks dimana jumlah baris = jumlah kolom
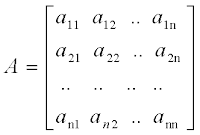
A : matriks bujur sangkar berukuran n x n
Diagonal utama A : a11, a22, ….., ann
Contoh :
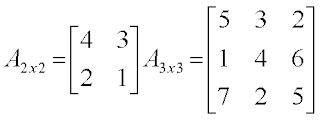
Matriks Diagonal :
Matriks bujur sangkar dimana elemen-elemen pada diagonal utamanya tidak semua elemennya nol, sedangkan unsur-unsur yang lain adalah nol
Contoh :
Matriks Satuan (Matriks Identitas) :
Matriks bujur sangkar di mana elemen-elemen pada diagonal utamanya masing-masing adalah satu, sedangkan elemen-elemen yang lain adalah nol.
Contoh:
Contoh Soal:
Bentuk Matriks Khusus
Matriks bujur sangkar
Suatu matriks dimana jumlah baris = jumlah kolom
A : matriks bujur sangkar berukuran n x n
Diagonal utama A : a11, a22, ….., ann
Contoh :
Matriks Diagonal :
Matriks bujur sangkar dimana elemen-elemen pada diagonal utamanya tidak semua elemennya nol, sedangkan unsur-unsur yang lain adalah nol
Contoh :
Matriks Satuan (Matriks Identitas) :
Matriks bujur sangkar di mana elemen-elemen pada diagonal utamanya masing-masing adalah satu, sedangkan elemen-elemen yang lain adalah nol.
Contoh:
Matriks Singular
Matriks bujur sangkar yang tidak mempunyai invers (berarti : nilai determinannya = 0)
Matriks Non Singular
Matriks bujur sangkar yang mempunyai invers (berarti: nilai determinannya 0)
Matriks Transpose
Bila matriks A berordo mxn, maka At (Transpose Derit) berordo nxm dengan
elemen baris ke I dan kolom ke j dari A1 adalah elemen baris ke j dan kolom ke I dari A
Matriks Idempotent
Matriks bujur sangkar dimana berlaku A2 = A atau An = A untuk suatu n, bila n = 2, 3, 4,….
Contoh:
Matriks Idempotent
Matriks bujur sangkar dimana berlaku A2 = A atau An = A untuk suatu n, bila n = 2, 3, 4,….
Contoh:
Program MAPLEnya:
# A = Matriks Idempotent, sehingga A2 = A
> Restart:
> A:=matriks([[2,-2,-4], [-1,3,4], [1,-2,-3]])
> C: = evalm (A&*A);
Matriks Nilpotent
Matriks bujur sangkar dimana berlaku A3 = 0 atau An = 0 untuk suatu n, bila n = 2, 3, 4,…..
Contoh:
Matriks nilpotent dari ordo 3 x 3
Program MAPLEnya:
# Matriks Nilpotent, sehingga
> Restart
> A:=matriks([[1,1,3],[5,2,6],[-2,-1,-3]]);
> evalm(A&*A*A);
Sifat Matriks Identitas dan Matriks Nol
Jika A = matriks berukuran n x n
I . A = A . I = A
A + 0 = 0 + A = A
A . 0 = 0 . A = 0
Matriks Segitiga (Triangular Matrix)
Matriks segitiga atas:
Matriks bujur sangkar, apabila setiap unsur yang terletak di bawah diagonal utamanya sama dengan nol
Contoh:
Matriks Segitiga Bawah
Matriks bujur sangkar dimana setiap unsurnya yang terletak diatas diagonal utamanya sama dengan nol
Contoh:
Operasi Aljabar Matriks
Penjumlahan dua matriks
A + B = (aij + bij)
A – B = (aij – bij)
Syarat penjumlahan dua matriks atau pengurangan dua matriks adalah mempunyai ordo yang sama
Contoh:
Penjumlahan dua matriks
A + B = (aij + bij)
A – B = (aij – bij)
Syarat penjumlahan dua matriks atau pengurangan dua matriks adalah mempunyai ordo yang sama
Contoh:
Program MAPLEnya:
# Penjumlahan Dua Matriks
> restart;
> A:=matrix([[5,6,7],[8,3,4]]);
> A:= matrikx(2,3,[5,6,7,8,3,4]);
Program MAPLEnya:
# Penjumlahan Dua Matriks
> restart;
> A:=matrix([[5,6,7],[8,3,4]]);
> A:= matrikx(2,3,[5,6,7,8,3,4]);
Program MAPLEnya:
# Penjumlahan Dua Matriks
> restart;
> A:=matrix([[5,6,7],[8,3,4]]);
> A:= matrikx(2,3,[5,6,7,8,3,4]);







1 komentar:
Contohnya ngak jelas
Posting Komentar